- Yazar Matthew Elmers [email protected].
- Public 2024-01-11 10:48.
- Son düzenleme 2025-01-24 09:38.
Bu yazıda Bayern, Rivenge ve Pennsylvania zırhlılarının toplarının zırh nüfuzunu ve Alman, Amerikan ve İngiliz zırhlarının karşılaştırmalı kalitesini anlamaya çalışacağız. Bunu yapmak son derece zor, çünkü Amerikan 356-mm, Alman 380-mm ve İngiliz 381-mm topları hakkındaki veriler çok kabataslak ve eksik ve bazen birbiriyle çelişiyor, ama yine de deneyeceğiz.
Sorun tam olarak nedir? Deniz kuvvetleri (sadece değil) tarihinin çoğu hayranının belirli silahların zırh nüfuzunu nasıl karşılaştırdığını görelim. Örneğin: örneğin İngiliz dretnotlarına ayrılmış bir yayında, Birinci Dünya Savaşı'nın 381 mm'lik bir İngiliz mermisinin yaklaşık 70 kablo mesafesinde 381 mm zırh plakasını deldiği bilgisi var. Zaten Alman "sermayesi" gemilerine ayrılmış başka bir baskıda - benzer bir Alman 380 mm mermisinin sadece 67, 5 kabloyla 350 mm zırhı "usta ettiği". Bundan İngiliz topunun daha güçlü olduğu anlaşılıyor - bu tam olarak varılan sonuç.
Ancak gerçekte, bu gibi verileri bu şekilde karşılaştırmak, ortalığı karıştırmak çok kolaydır.
Yukarıdaki veriler gerçek atış sonucu mu elde ediliyor yoksa zırh delme teknikleri kullanılarak mı hesaplanıyor? Bunlar gerçek atışın sonuçlarıysa, koşullar her iki silah için de aynı mıydı? Zırh penetrasyonu hesapla elde edilmişse, aynı yöntemler kullanılmış mıydı? Elde edilen veriler ilgili bakanlık ve bakanlıklardan uzmanların çalışmalarının sonucu mu yoksa hesap makinesi almış tarihçilerin yaptığı hesaplamaların sonucu mu? Açıktır ki, ikinci durumda doğruluk çok daha düşük olacaktır… Örnekler için çok uzağa gitmenize gerek yok: S. Vinogradov'un ünlü monografisini ele alalım, "İkinci Reich'ın Süperdretnotları" Bayern "ve" Baden ". Ek No. 2'de, saygın tarihçi V. L. Kofman, Rivenge ve Bayern zırhlılarının yeteneklerini karşılaştırmak için büyük miktarda hesaplama yapıyor. Ancak ne yazık ki, 15 inçlik silahlar için parametre tablosuna bakmak yeterlidir (s. 124) ve saygın yazarların hesaplamalarına göre, yükseklik açısı 20 olan bir İngiliz 381 mm silahın, 25 derece, yalnızca 105 kablo aralığına sahiptir, yani yaklaşık 19, 5 bin m. Aynı başlangıç hızı (732 m / s) ve biraz daha düşük bir yükseklik açısı (20 derece) için yabancı kaynaklar önemli ölçüde daha büyük mesafeler verirken - 21, 3-21, 7 bin m Tabii ki ancak gerçek değerlerden bu tür sapmalar hesaplama sonuçlarına en olumsuz etkiyi yapıyor.
Ancak kaynaklar, doğruluğu şüphe götürmeyen uzmanların hesaplamalarının sonuçlarını sunsa bile, karşılaştırmayı zorlaştıran başka bir faktör ortaya çıkıyor: Buradaki nokta zırhın kalitesi. Aynı İngilizlerin, belirli bir dretnot tasarlarken zırh nüfuzunu hesaplarken, karşılık gelen İngiliz zırhı göstergelerini, Almanları - sırasıyla Almanları, vb. kullandığı açıktır. Ve farklı ülkelerin zırhları dayanıklılık açısından farklılık gösterebilir, ancak bu hala sorunun yarısıdır: sonuçta, tek bir ülkede aynı Krupp zırhı sürekli olarak geliştiriliyordu. Böylece, örneğin İngiltere'de ve görünüşe göre aynı Krupp zırhı için, ancak farklı zamanlarda yapılan topçu sistemlerinin hesaplamalarının karşılaştırılamaz olduğu ortaya çıkıyor. Ve buna, dünyanın çeşitli ülkelerinde zırh kasasının evrimi üzerine ciddi çalışmaların neredeyse tamamen yokluğunu da eklersek …
Genel olarak, zırh nüfuzunun az çok güvenilir bir karşılaştırması, ilk bakışta göründüğü kadar basit bir iş değildir. Ve dostane bir şekilde, bir meslekten olmayan (şüphesiz bu makalenin yazarıdır) bu konuyu ele almamak daha iyidir. Ancak, ne yazık ki - derin üzüntümüze göre, profesyoneller bir şekilde bu sorunlarla uğraşmak için acele etmiyorlar, bu yüzden … dedikleri gibi, damgalı kağıt yokluğunda düz metin yazıyoruz.
Tabii ki, yukarıda belirtilen topçu sistemlerinin tam ölçekli testlerini yapmak artık mümkün değil, dolayısıyla kaderimiz hesaplamalar. Ve eğer öyleyse, zırh delme formülleri hakkında en az birkaç kelime söylemek gerekir. Modern hesaplama yöntemleri yayınlanırsa, yalnızca kapalı sürümlerde ve popüler literatürde genellikle Jacob de Marr formülü verilir. Deniz Harp Okulu Profesörü L. G. Goncharov, 1932 topçu ders kitabında buna Jacob de Marr formülü adını verdi. Bu formül, diğerleri ile birlikte, geçen yüzyılın başında yaygındı ve söylemeliyim ki, oldukça doğru - belki de o yılların benzer formülleri arasında en doğru olanıdır.
Özelliği, fiziksel olmaması, yani fiziksel süreçlerin matematiksel bir açıklaması olmamasıdır. De Marr'ın formülü ampiriktir, demir ve çelik-demir zırhın deneysel bombardımanının sonuçlarını yansıtır. Bu "bilimsel olmayan doğasına" rağmen, de Marr'ın formülü, atışın ve Krupp zırhının gerçek sonuçlarına diğer yaygın formüllerden daha iyi bir yaklaşım gösterdi ve bu nedenle hesaplamalar için kullanacağız.
İlgilenenler bu formülü bu makalenin ekinde bulacaklar, ancak bu materyali okuyan herkesi onu anlamaya zorlamaya gerek yok - bu makalenin sonuçlarını anlamak için gerekli değil. Yalnızca, hesaplamanın askeri filoların tarihiyle ilgilenen herkes için çok basit ve tanıdık kavramlar kullandığını not ediyoruz. Bunlar merminin kütlesi ve kalibresi, zırhın kalınlığı, merminin zırha çarptığı açı ve merminin zırh plakasına çarptığı andaki hızıdır. Ancak de Marr elbette kendisini yukarıdaki parametrelerle sınırlayamazdı. Sonuçta, bir merminin nüfuzu sadece kalibresine ve kütlesine değil, aynı zamanda bir dereceye kadar şekline ve yapıldığı çeliğin kalitesine de bağlıdır. Ve merminin üstesinden gelebileceği zırh plakasının kalınlığı, elbette sadece merminin performansına değil, aynı zamanda zırhın kalitesine de bağlıdır. Bu nedenle, de Marr, formüle, aslında belirtilen zırh ve mermi niteliklerini dikkate almak üzere tasarlanmış özel bir katsayı ekledi. Bu katsayı, zırh kalitesindeki artışla yükselir ve merminin şekli ve kalitesindeki bozulma ile azalır.
Nitekim, farklı ülkelerin topçu sistemlerini karşılaştırmanın ana zorluğu, tam da gelecekte (K) diyeceğimiz bu katsayıya "dayanmaktadır". Yukarıdaki araçların her biri için onu bulmamız gerekecek - tabii ki biraz doğru bir sonuç almak istiyorsak.
Öyleyse, önce Alman 380-mm / 45 top "Bayern" in zırh nüfuzu hakkında oldukça yaygın verileri alalım, buna göre 12.500 m mesafedeki topun (aynı 67, 5 kablolar) 350 mm'ye nüfuz edebileceğine göre zırh. Zırh üzerindeki etki anında 800 m / s başlangıç hızıyla 750 kg'lık bir merminin parametrelerini bulmak için balistik bir hesap makinesi kullanıyoruz: böyle bir merminin kesinlikle dikey olarak yerleştirilmiş bir zırh plakasına çarpacağı ortaya çıkıyor. 505,8 m/sn hız ile 10,39 derecelik bir açı. Küçük bir sorumluluk reddi - bundan sonra, merminin çarpma açısı hakkında konuştuğumuzda, sözde "normalden açı" demek istiyoruz. "Normal", merminin bonneplite yüzeyine kesinlikle dik, yani 90 derecelik bir açıyla çarpmasıdır. Buna göre, mermi 10 derecelik bir açıyla çarptı.normalden, levhaya 80 derecelik bir açıyla çarptığı anlamına gelir. "referans" dan 90 derece saparak yüzeyine. 10 derece.
Ancak Alman silahının zırh nüfuzuna geri dönelim. Bu durumda (K) katsayısı yaklaşık olarak (en yakın tam sayıya yuvarlanır) 2.083'e eşit olacaktır - bu değer Birinci Dünya Savaşı döneminin zırhı için oldukça normal kabul edilmelidir. Ancak burada bir sorun ortaya çıkıyor: gerçek şu ki, zırh nüfuzu ile ilgili veri kaynağı, Bayern'in 380-mm / 45 topunun zırhlının ana kalibresi ile karşılaştırıldığı "İkinci Dünya Savaşı'nın Alman Başkent Gemileri" kitabıdır. "Bismark". Ve hesaplama, iki dünya savaşı arasındaki aralıkta yaratılan ve Bayenne, Rivenge ve Pennsylvania'ya kurulandan çok daha güçlü olan Krupp zırhının göstergelerini hesaba katmamış olabilir mi? Ayrıca, elektronik ansiklopedi navweaps, 20.000 m mesafedeki Alman 380 mm mermilerin 336 mm zırh plakasına nüfuz edebildiğine dair kanıtlar olduğunu ve Birinci Dünya Savaşı döneminin zırhından bahsettiğimizi bildiriyor.
Eh, inanıyoruz: 20 km'de geliş açısı 23.9 derece olacak, merminin zırh üzerindeki hızı 410.9 m / s ve katsayısı (K) - zırha uymayan bazı talihsiz 1618 Birinci Dünya Savaşı'nın tüm çağında direnç değerleri. Benzer bir sonuç genellikle Alman yapımı Krupp zırhını homojen zırh direncine yaklaştırıyor… Açıkçası, navweaps verileri bir tür hata içeriyor.
O halde başka bir bilgi kaynağı kullanmayı deneyelim. Şimdiye kadar hesaplanan verileri kullandık ve şimdi bunları Alman 380-mm / 45 topunun gerçek testlerinin sonuçlarıyla karşılaştırmaya çalışacağız: bunlar S. Vinogradov tarafından yukarıda bahsedilen Almancaya ayrılmış monografta verilmiştir. savaş gemileri.
200, 290 ve 450 mm kalınlığındaki zırh plakalarına karşı zırh delici mermilerle yapılan 3 atışın sonuçlarını açıklar, ikincisi bizim için en ilginç olanı: 734 kg ağırlığındaki bir mermi zırh plakasına 0 açıyla çarptı (yani yüzeye 90 derece açıyla) ve 551 m/s hızla 450 mm levhadan delinir. Benzer bir sonuç (K) 1 913 katsayısına karşılık gelir, ancak aslında biraz daha düşük olacaktır, çünkü Almanlar mermilerini deldikleri engelin 2 530 m kadar gerisinde bulmuşlardır ve - genel olarak. Ne yazık ki, merminin bu mesafenin ne kadarının havada uçtuğuna, ne kadar - yerde "sürdüğüne" dair herhangi bir veriye sahip olmadan, zırh nüfuzundan sonra depoladığı enerjiyi belirlemek kesinlikle imkansızdır.
Şimdi İngiliz 381 mm/42 topçu sistemini ele alalım. Ne yazık ki, zırh nüfuzu hakkındaki veriler oldukça belirsiz: örneğin, V. L. Kofman'a göre, bu İngiliz silahlarının zırhı deldiğinden, kendi kalibrelerinin kalınlığında yaklaşık 70 kablo mesafesinden söz ediliyor. Ama hangi mermiyle ve hangi başlangıç hızıyla? Referansın savaş kruvazörü "Hood" a adanmış monografta yer aldığı ve bu geminin yaratılış dönemine atıfta bulunduğu göz önüne alındığında, 871 kg'lık bir mermiden bahsettiğimiz varsayılabilir. Ancak burada başka bir soru ortaya çıkıyor: Böyle bir merminin resmi başlangıç hızı 752 m / s idi, ancak İngilizler tarafından bazı hesaplamalar 732 m / s gibi daha düşük bir hızda yapıldı, peki hangi değeri almalıyız? Ancak belirtilen hızlardan hangisini alırsak alalım, (K) katsayısı 1 983 - 2 048 arasında dalgalanacaktır ve bu, Alman topunun (K) değeri için hesapladığımızdan daha yüksektir. Bunun, Alman zırhına kıyasla İngiliz zırhının kalitesinin üstünlüğünden bahsettiği varsayılabilir … yoksa Alman mermisinin geometrik şekli zırhı delmek için daha mı uygun? Ya da belki de bütün mesele şu ki, V. L. Kofman hesaplanmış değerlerdir, ancak pratikte İngiliz mermileri daha iyi bir sonuç elde eder mi?
"Baden" savaş gemisinin bombalanmasının sonuçları hakkında elimizde veri var.

Yani, İngiliz mermilerinden biri, 18 derecelik bir açıyla vuruyor. 472 m / sn hızında, Alman ana kalibreli taretinin 350 mm ön zırhını "güçlendirdi". Bu veriler çok daha değerli çünkü bu durumda İngiliz değil, Alman zırhı bombardımana maruz kaldı, yani 381-mm / 42 ve 380-mm / 45 silahlarının testleri tek bir koordinat sisteminde..
Ne yazık ki, bize çok fazla yardımcı olmuyorlar. İngiliz mermisinin Alman kulesini dedikleri gibi “son güçle” deldiğini varsayarsak ve 351 mm zırh olsaydı başarısız olurdu, o zaman (K) 2.021'e eşit olurdu. bu arada, S. Vinogradov'un Alman kulesinin 350 mm ön zırhını delen İngiliz mermisinin daha sonra bulunmadığını belirtmesi ilginç, ama aslında rapor başka bir şey söylüyor - patladı ve parçaların kulede nereye uçtuğunun açıklaması.
Tabii ki, bu penetrasyonun 381 mm'lik bir mermi için sınır olduğunu, hatta buna yakın olduğunu varsaymak için mutlak bir dayanağımız yok. Ancak yine de, bazı dolaylı işaretlere göre, durumun tam olarak böyle olduğu varsayılabilir. Bir başka vuruş da buna “ipuçları” veriyor: 871 kg'lık bir İngiliz mermisi, 350 mm'lik bir barbete 11 derecelik bir açıyla vuruyor, ancak zırhta 40 cm çapında bir delik açabilmesine rağmen, barbetin içine girmedi. kendisi, zırhın üstesinden gelme sürecinde patladı. Bu durumda, vuruş neredeyse barbetin tam ortasında meydana geldi, yani zırh plakasının eğriliği, herhangi bir etkisi varsa, en düşük seviyedeydi.
Yukarıdakilerin hepsinden, bazı sonuçlar çıkarmaya çalışılabilir, ancak kanıt temelinin kırılganlığı nedeniyle, elbette, doğaları gereği çok varsayımsal olacaktır.
Sonuç 1: Birinci Dünya Savaşı sırasındaki Alman zırhı, dayanıklılık açısından İngilizlerle kabaca eşleşti. Bu sonuç, V. L.'nin ifadesi geçerliyse geçerlidir. Kofman, İngiliz 381 mm / 42 topunun kalibresine eşit 70 kbt zırhı delme yeteneğine sahip olduğunu ve Alman taretinin ön plakasının 350 mm'sinin 18'lik bir açıyla nüfuz ettiği varsayımında yanılmıyorsak derece ve 472 m/s hız… İngiliz 381 mm mermisinin nüfuz sınırı veya buna çok yakın.
Sonuç 2. Görünüşe göre, Alman 380 mm mermisinin şekli ve kalitesi, ona İngiliz mermisinden daha iyi zırh nüfuzu sağladı. Yukarıdaki verilere dayanarak, Alman zırhına ateş ederken İngiliz 381 mm mermisinin katsayısının (K) yaklaşık 2.000, Alman 380 mm mermisinin ise yaklaşık 1.900 olduğunu varsayabiliriz. İngiliz ve Alman zırhlarının zırh direnci yaklaşık olarak eşdeğerdir, düşük katsayının (K) tek nedeninin yalnızca merminin kendisi olabileceği açıktır.
Bir Alman kabuğu neden daha iyi olabilir? Kalibresi bir milimetre biraz daha küçüktür, ancak elbette bunun önemli bir etkisi olamaz. Hesaplama, aynı kütle (750 kg) ile kalibrede 1 milimetrelik bir değişikliğin zırh nüfuzunda 1.03 milimetre artışa yol açacağını göstermektedir. Alman mermisi de daha kısa - uzunluğu 3.5 kalibreydi, İngiliz "Greenboy" uzunluğu ise 4 kalibreydi. Başka farklılıklar da olmuş olabilir. Elbette merminin yapıldığı çeliğin kalitesi burada önemli bir rol oynuyor.
Şimdi, 75 kablo mesafesi için Alman ve İngiliz silahlarının zırh nüfuzunu hesaplayalım - kesin bir savaş için genel olarak kabul edilen bir mesafe, hatta bir düşman gemisini yok etmeye yetecek kadar isabetin beklenebileceği bir mesafe.
Belirtilen mesafede, 752 m / s başlangıç hızında ateşlenen 871 kg İngiliz 381-mm / 42 top mermisi, dikey olarak yerleştirilmiş zırh plakasına 13.05 derecelik bir açıyla ve hızı "plaka üzerinde" çarptı. 479,6 m/sn idi… Jacob de Marr'ın formülüne göre (K) 2.000'e eşit olduğunda, İngiliz mermisinin zırh nüfuzu 376, 2 mm idi.
Alman kabuğuna gelince, her şey biraz daha karmaşık. Zırh penetrasyonu açısından İngilizceyi aştığına dair sonucumuz doğruysa, o zaman Alman 380-mm / 45 topunun 75 kablo üzerindeki yetenekleri İngiliz on beş inçlik topa çok yakındı. Bu mesafede, Alman 750 kg mermi hedefi 12.42 derecelik bir açıyla 482,2 m / s hızında vurdu ve (K) 1,900'e eşit, zırh nüfuzu 368,9 mm idi. Ancak bu makalenin yazarı hala yanılıyorsa ve Alman silahı için İngiliz silahıyla aynı katsayıyı kullanmaya değerse, 380 mm merminin yetenekleri 342,9 mm'ye düşer.
Bununla birlikte, yazara göre, Alman mermisinin zırh nüfuzu 368, 9 mm'ye en yakın (sonuçta, merminin 2,5 km uçmasına rağmen pratik ateşleme 1913 katsayısı verdi), ancak zırh nüfuzu İngiliz mermisi biraz daha düşük hesaplanabilir. Genel olarak, 75 kablo mesafesinde, İngiliz ve Alman topçu sistemlerinin zırh penetrasyonu açısından oldukça karşılaştırılabilir olduğu düşünülebilir.
Ancak Amerikan 356 mm / 45 topuyla her şey çok daha ilginç çıktı. 680 kg ağırlığındaki mermiler için daha önce belirtilen veriler, Rus dili literatüründe kanonik olarak kabul edilmelidir.
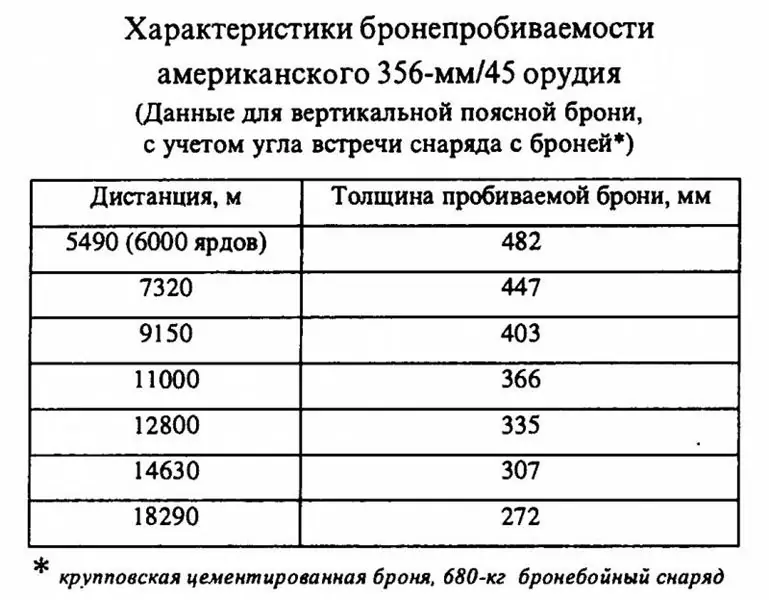
Nitekim, içinde belirtilen değerler tamamen açık sonuçlara yol açıyor gibi görünüyor: 1923'ten sonra Amerika Birleşik Devletleri'nde ortaya çıkan 680 kg'lık mermiler bile, 380-381-mm Avrupa'larına göre zırh penetrasyonunda daha düşükse " meslektaşları", o zaman 356 mm Amerikan dretnotları ile donatılmış daha önceki 635 kg'lık mermiler hakkında gerçekten ne konuşuyorsunuz! Daha hafiftirler, yani uçuşta daha hızlı hız kaybederler, ilk hızları daha ağır mermileri geçmez ve şekil ve kalite açısından 1923 mühimmatının bir avantajı olmalıdır. Hizmete girdiği sırada Amerikan "Pensilvanya" nın İngiliz ve Alman dretnotlarına zırh nüfuzu açısından daha düşük olduğu gün gibi açıktır. Açık, değil mi?
Bu, yazarın ABD, Almanya ve İngiltere'nin "Standart" zırhlıları makalesindeki Amerikan on dört inçlik silahlarının yeteneklerini göz önünde bulundurarak yaptığı sonuçtur. Amerikan "Pensilvanya" ". Ve sonra bir hesap makinesi aldı …
Gerçek şu ki, de Marra formülüne göre hesaplama, Amerikan 356-mm / 45 toplarının tabloda belirtilen zırh penetrasyonunun 2.317'ye eşit (K) katsayısına sahip olduğunu gösterdi! Başka bir deyişle, tabloda gösterilen Amerikan 680 kg mermiler, Birinci Dünya Savaşı döneminde yaratılmayan zırhlara maruz kaldığında, ancak çok daha sonra ve daha dayanıklı örneklerde sonuçları gösterdi.
Birinci ve ikinci dünya savaşları arasındaki dönemde zırh korumasının gücünün ne kadar arttığını söylemek zor. Rus dilindeki kaynaklarda, Krupp'un zırhının gücünün yaklaşık% 20-25 oranında arttığı varsayılabileceğine dayanarak, bu konuyla ilgili yalnızca kısa ve genellikle çelişkili referanslar vardır. Bu nedenle, Birinci Dünya döneminin büyük kalibreli mermileri için, katsayısının (K) büyümesi 1.900 - 2.000 ila 2.280 - 2.500 arasında olacaktır, ancak burada, zırh koruma kalitesinde bir artışla birlikte unutulmamalıdır., elbette, mermilerin kalitesi de arttı ve bu nedenle İkinci Dünya Savaşı'nın (K) ağır Mühimmatı için daha az olabilir. Bu nedenle, (K) savaş sonrası mermiler için, daha önce kazanılan deneyimler dikkate alınarak doğal olarak geliştirilmiş, oldukça organik görünüyor, ancak İkinci Dünya Savaşı döneminin zırhı için ilk değil.
Ancak, 680 kg'lık Amerikan mermileri için (K) katsayısını 2.000 seviyesine ayarlayarak, yani zırh koruma kalitesini Birinci Dünya Savaşı dönemine getirerek, 75 kablo mesafesi için zırh alacağız. 393,5 mm seviyesinde nüfuz, yani İngiliz ve Alman on beş inçlik toplarından daha yüksek!

635 kg mermiye dönüştürme, çok önemsiz bir düzeltme sağlar - balistik hesap makinesi, 10, 82 derecelik bir insidans açısına sahip 75 kablo mesafesinde olduğunu gösterdi. ve "zırh üzerinde" 533, (K)'de 2 m 2.000'e eşit olan Amerikan mermisi, 380 mm kalınlığında Birinci Dünya Savaşı döneminin zırhına nüfuz eder, yani kendi kalibresinden önemli ölçüde daha fazla!
Öte yandan, böyle bir hesaplamanın hala tamamen doğru olmaması oldukça olasıdır. Gerçek şu ki, bazı raporlara göre, aynı zırh için (K) katsayısı, merminin kalibresindeki bir artışla azalır. Yani, örneğin, hesaplamalarımızda, Alman 380-mm / 45 topçu sistemi için hesaplama ile elde edilen ve kaynaklarda yayınlanan maksimum değer (K) 2.083'tür. Aynı zamanda, Alman 305-mm için hesaplamalar / Heligolands ile başlayan Kaiserlichmarine gemilerine monte edilen 50 silah, zırh delme ile ilgili kaynaklardan alınan veriler 2.145 seviyesinde (K) veriyor. Buna göre 356-mm / 45 silah (K) = 2.000 Amerikan silahlarının zırh nüfuzunu hesaplamak için aldık, hala çok küçük.
Buna ek olarak, ne yazık ki, yazarın Amerikan Krupp zırhının zırh direncini Avrupa muadilleriyle karşılaştırmak için herhangi bir "ipucu" yok. Alman ve İngiliz zırh korumasına eşdeğer olduğunu düşünmekten başka bir şey kalmadı, ancak bu elbette böyle olmayabilir.
Tüm bu oldukça kaotik verileri özetleyelim. Hesaplamalarda kullanılan "yöntemlerin" hataları dikkate alındığında, yüksek bir olasılıkla şu varsayılabilir: Rivenge, Bayern ve Pennsylvania zırhlılarının ana kalibreli silahlarının 75 kablo mesafesindeki dikey zırh korumasının zırh nüfuzu yaklaşık olarak aynıydı ve yaklaşık 365-380 mm idi.
Bir dizi varsayıma rağmen, elimizdeki veriler hala dikey zırh korumasıyla ilgili bazı sonuçlar çıkarmamıza izin veriyor. Ancak zırhlı güverteler olan yatay bariyerleri aşmak ile her şey çok daha karmaşık. Gerçek şu ki, Jacob de Marr, ne yazık ki, yatay savunmanın gücünü belirlemek için bir formül oluşturmaya hiç zahmet etmedi. Modern zırh türlerine uyarlanmış temel formülü, yalnızca kalınlığı 75 mm'den fazla olan çimentolu zırhı hesaplamak için uygundur. Bu formül, bu makalenin 1 No'lu Ekinde verilmiştir ve makaledeki önceki tüm hesaplamalar bu formül kullanılarak yapılmıştır.
Ancak o yılların gemilerinin güverteleri çimentolu (heterojen) değil, yüzeyi sertleştirilmiş bir tabaka içermeyen homojen zırhla korunuyordu. Bu tür zırhlar için (ancak - dikey olarak monte edilmiş!), 75 mm'den daha az kalınlığa sahip çimentosuz zırh plakalarını değerlendirmek için farklı bir formül kullanılır, Ek No. 2'de verilmiştir.
Bu formüllerin her ikisinin de ciddi bir kaynaktan alındığını belirtmek isterim: “Deniz taktiklerinin seyri. Topçu ve Zırh 1932, yazar - RKKA Deniz Harp Okulu L. G. Goncharov, savaş öncesi SSCB'nin deniz topçuları alanında önde gelen uzmanlarından biri.
Ve ne yazık ki hiçbiri yatay korumanın dayanıklılığını değerlendirmek için uygun değil. Çimentolu zırh için formülü kullanırsak, 75 kablo mesafesinde yetersiz zırh nüfuzu elde ederiz: 381 mm / 42 İngiliz için 46,6 mm, 380 mm / 45 Alman için 39,5 mm ve 356 mm / 45 Amerikan için 33.8 mm silahlar. Çimentosuz zırh için ikinci formülü kullanırsak, 75 kablo mesafesi için tipik bir açıyla vurulduğunda, üç topçu sisteminin tümü 74 mm zırh plakasına kolayca nüfuz eder ve ardından büyük bir kinetik enerji kaynağı korur - örneğin, İngiliz 381- mm, 75 kablo mesafesinde bu kalınlıktaki zırhı delmek için bir mermi 264,5 m / s hıza sahipken, hızı 482,2 m / s olacaktır. Zırh plakasının kalınlığındaki sınırlamayı göz ardı edersek, yukarıdaki formüle göre İngiliz 381 mm mermisinin 180 mm'den fazla kalınlığa sahip güverte zırhını delebildiği ortaya çıkıyor! Hangi, elbette, tamamen imkansız.
Bayern sınıfı zırhlının test sonuçlarına atıfta bulunmaya çalışırsak, zırh delici 871 kg İngiliz mermilerinin, 100 mm kalınlığındaki kulelerin yatay zırhına 11 derecelik bir açıyla iki kez çarptığını göreceğiz. başlangıç hızı 752 m/s olan bir mermi için 67,5 kablo mesafesine ve başlangıç hızı 732 m/s olan bir mermi için 65 kablo mesafesine karşılık gelir. Her iki seferde de zırh delinmedi. Ancak bir durumda, mermi, sekme, zırhta 70 cm derinliğe sahip bir oluk yaptı, yani plaka çok güçlü bir şekilde büküldü. Ve ikincisinde, kabuk yine sekmiş olsa da, zırh sadece 10 cm içbükey değil, aynı zamanda yırtılmıştı.

Hasarın benzer doğası, Alman 100 mm zırhının belirtilen mesafelerde koruma sağlamasına rağmen, mümkün olanın sınırında olmasa da buna çok yakın olduğunu gösteriyor. Ancak, çimentolu zırh formülüne göre hesaplama, gelme açısının daha yüksek olacağı daha büyük bir mesafede sadece 46,6 mm'lik zırh nüfuzu sağlar ve buna göre merminin güverte zırhını delmesi daha kolay olur. Yani, formüle göre, 100 mm'lik güvertenin şaka olarak ve büyük bir güvenlik marjıyla İngiliz mermilerini yansıtması gerektiği ortaya çıktı - ancak uygulama bunu doğrulamıyor. Aynı zamanda, çimentosuz zırh formülünü kullanan hesaplamalara göre, Baden'in ana kalibresinin çatılarının kolayca delinmesi gerektiği ve - büyük bir kabuk enerjisi kaynağı ile - ki bu yine değil. tamamen pratikle doğrulandı.
Hesaplamalardaki bu tür yanlışlıkların tamamen mantıklı bir açıklaması olduğunu söylemeliyim. Daha önce de söylediğimiz gibi, de Marr'ın formülleri fiziksel süreçlerin matematiksel bir tanımı değil, sadece zırhı test ederken elde edilen kalıpların bir sabitlenmesidir. Ancak yatay değil dikey zırh koruması test edildi ve bu durumda kalıpların çalışmayı durdurması hiç de şaşırtıcı değil: mermilerin yüzeylerine çok küçük bir açıyla çarptığı yatay olarak yerleştirilmiş zırh için, bu kalıplar, elbette tamamen farklıdır.
Bu makalenin yazarı, de Marr'ın formüllerinin normalden 60 dereceden fazla olmayan, yani 30 dereceden levha yüzeyine ve daha fazlasına kadar olan sapma açılarında etkili bir şekilde çalıştığı "internette" görüşlere rastladı. Bu değerlendirmenin gerçeğe çok yakın olduğu varsayılabilir.
Bu nedenle, yazara sunulan matematiksel aygıtın, Rivenge, Bayern ve Pennsylvania zırhlılarının yatay koruma direncinin güvenilir bir şekilde hesaplanmasına izin vermediğini üzülerek belirtmeliyiz. Yukarıda belirtilenler ışığında, çeşitli kaynaklarda verilen yatay zırhın zırh nüfuzu hakkındaki verileri kullanmak zor olacaktır - kural olarak, hepsi de Marr'ın formüllerine göre aynı hesaplamalara dayanmaktadır ve yanlıştır.






